[카테고리:] 노트

도입

음악이나 음성을 이미지 처럼 다루려면 어떻게 해야 할까요? 이미지는 픽셀 값이 2차원 격자 형태로 배열되지만, 오디오는 시간에 따라 변하는 1차원 신호 입니다.

오디오 입력 표현에는 원시 파형을 그대로 쓰는 접근과, 시간-주파수 표현으로 변환해 2차원 격자 입력으로 다루는 접근이 있습니다.

멜 스펙트로그램(Mel Spectrogram)은 오디오 신호를 시간-주파수의 2차원 표현으로 변환합니다. 이 변환을 거치면 CNN이나 Vision Transformer 등 이미지 기반 모델을 오디오 분석에 활용할 수 있습니다.

이 글에서는 멜 스펙트로그램이 어떻게 만들어지는지, 왜 “멜” 스케일을 사용하는지, 그리고 모델 입력으로 쓰기 위해 어떤 후처리가 필요한지 다루고, librosa로 직접 구현해봅니다.

시각화에서는 librosa에서 제공하는 트럼펫 샘플을 사용했으며, 글 마지막에 파라미터를 직접 바꿔가며 실험해볼 수 있는 실습 코드 레포지토리도 준비했습니다.

1. 배경: 소리와 주파수

파형: 시간 영역의 표현

소리는 공기의 진동입니다. 마이크는 이 진동을 전기 신호로 바꾸고, 컴퓨터는 이를 일정 간격으로 샘플링하여 숫자의 나열로 저장합니다. 이것이 파형(waveform)입니다.

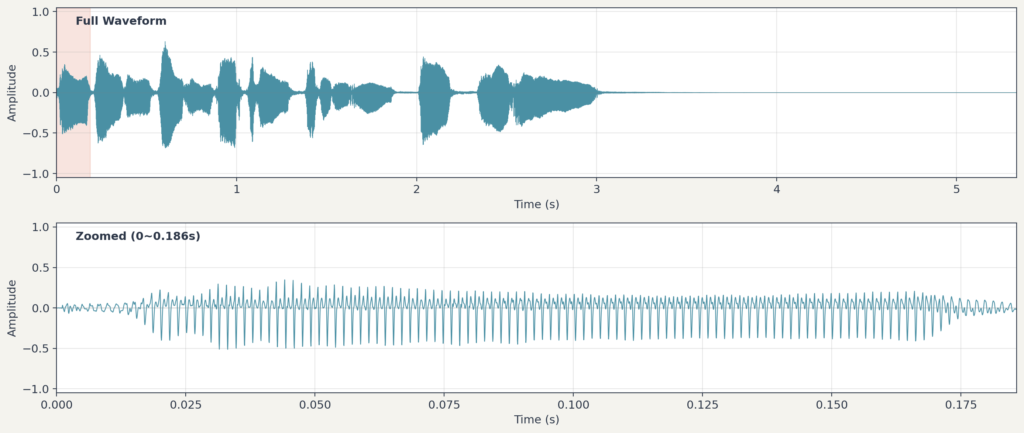
CD 품질 오디오는 초당 44,100개의 샘플을 기록합니다($\text{44.1kHz}$). 1분짜리 모노 오디오는 약 265만 개($44,100\times60$)의 숫자로 이루어집니다. 스테레오는 채널이 2개이므로 그 두 배입니다. 이 글의 예시는 $\text{22,050Hz}$를 사용합니다. librosa.load는 기본적으로 이 값으로 리샘플링을 하며, 원본 샘프레이트를 유지하려면 $\text{sr=None}$을 지정합니다. 파형은 시간에 따른 진폭 변화를 보여주지만, 어떤 높낮이의 소리가 섞여 있는지는 직접 알려주지 않습니다.

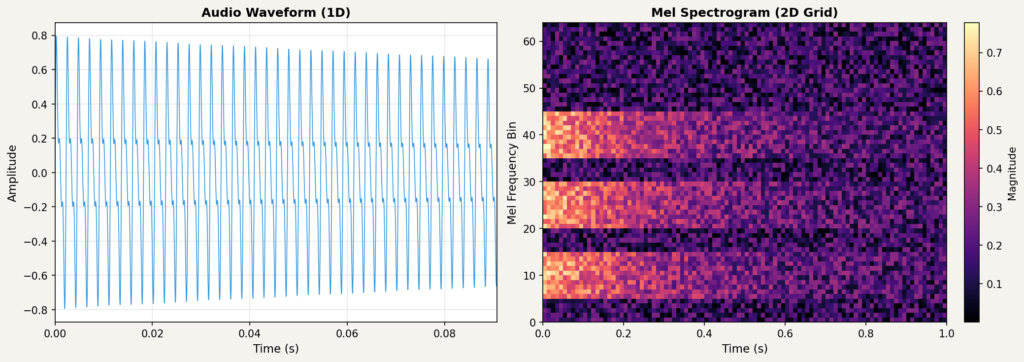
아래는 이 글에서 사용할 트럼펫 샘플의 음원과 그 파형입니다.

주파수: 소리의 높낮이

소리의 높낮이는 주파수로 결정됩니다. 주파수는 1초에 진동하는 횟수이고, 단위는 $\text{Hz}$(헤르츠)입니다. 피아노 가운데 ‘라’음은 약 $\text{440Hz}$, 즉 1초에 440번 진동합니다. 주파수가 높을수록 높은 음으로 들립니다.

실제 소리는 단일 주파수가 아니라 여러 주파수의 조합입니다. 바이올린과 플루트가 같은 음을 연주해도 다르게 들리는 이유는, 기본 주파수는 같지만 함께 섞인 배음(overtone)의 구성이 다르기 때문입니다.

파형만 보고는 어떤 주파수들이 얼마나 강하게 섞여 있는지 파악하기 어렵습니다. 이를 분석하는 도구가 푸리에 변환입니다.

푸리에 변환: 시간에서 주파수로

푸리에 변환(Fourier Transform)은 시간 영역의 신호를 주파수 영역으로 바꿔주는 수학적 도구입니다. 복잡하게 생긴 파형을 “이 신호는 $\text{100Hz}$ 성분이 이만큼, $\text{200Hz}$ 성분이 이만큼, …” 하는 식으로 분해합니다.

연속 신호에 대한 푸리에 변환은 다음과 같이 정의됩니다.

여기서 $x(t)$는 시간 영역 신호, $X(f)$는 주파수 $f$에서의 성분입니다. $e^{-i2\pi ft}$는 주파수 $f$의 복소 정현파로, 신호에서 해당 주파수 성분을 추출하는 역할을 합니다.

디지털 오디오는 이산 신호이므로, 이산 푸리에 변환(DFT)을 사용합니다. 길이 $N$ 인 신호에 대한 DFT는 다음과 같습니다.

$X[k]$의 절댓값 $|X[k]|$가 해당 주파수 성분의 크기(magnitude)입니다. 이를 제곱한 $|X[k]|^2$를 파워 스펙트럼(power spectrum)이라고 부릅니다.

예를 들어, $\text{440Hz}$ 기본음과 그 배음($\text{880Hz}$, $\text{1320Hz}$)을 합성한 신호를 생각해봅시다. 이 신호에 DFT를 적용하면, 세 주파수 지점에서 높은 크기(magnitude)가 나타나고, 이를 제곱하면 파워 스펙트럼이 됩니다. [그림 2]의 좌측은 세 사인파를 합성한 복잡한 파형이고, 우측은 푸리에 변환 결과로 $\text{440Hz}$, $\text{880Hz}$, $\text{1320Hz}$에서 피크가 나타납니다.

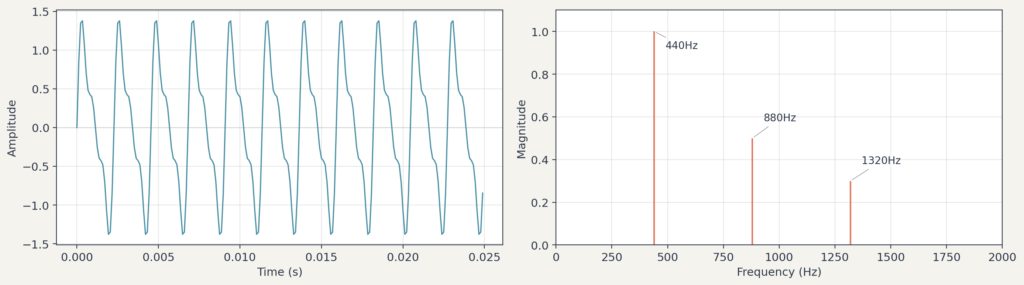
참고로, DFT(이산 푸리에 변환)는 변환의 정의이고, FFT(Fast Fourier Transform)는 DFT를 효율적으로 계산하는 알고리즘입니다.¹ 실무에서는 DFT를 FFT로 계산하는 것이 일반적입니다.

푸리에 변환의 결과는 신호 전체에 대한 평균적인 주파수 구성입니다. 음악처럼 시간에 따라 주파수 구성이 변하는 신호를 분석하려면, “언제 어떤 주파수가 강했는지”를 알아야 합니다. 이를 위해 STFT가 등장합니다.

2. STFT: 시간-주파수 분석

짧은 구간씩 나눠서 분석하기

STFT(Short-Time Fourier Transform, 단시간 푸리에 변환)는 신호를 짧은 구간(프레임)으로 나누고, 각 구간에 푸리에 변환을 적용하는 방법입니다. 이렇게 하면 시간에 따른 주파수 변화를 추적할 수 있습니다.

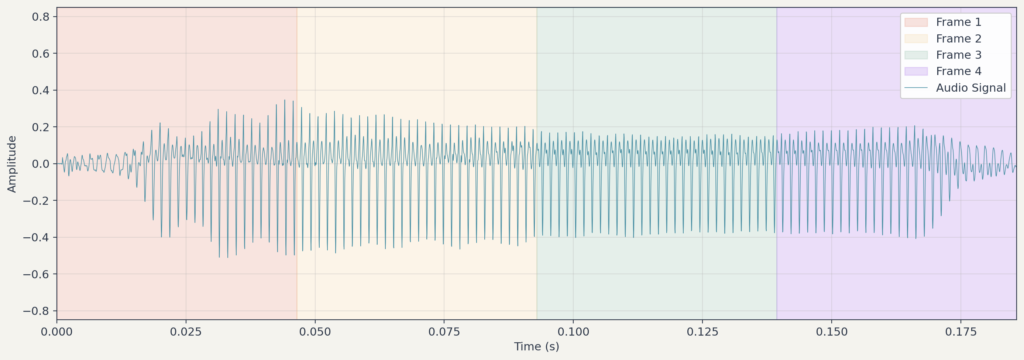
윈도우 함수

신호를 자를 때 그냥 뚝 자르면 문제가 생깁니다. 유한 길이로 자르면 경계의 불연속으로 인해 에너지가 인접 주파수로 퍼지는 현상이 발생합니다. 이를 스펙트럼 누설(spectral leakage)이라고 합니다.

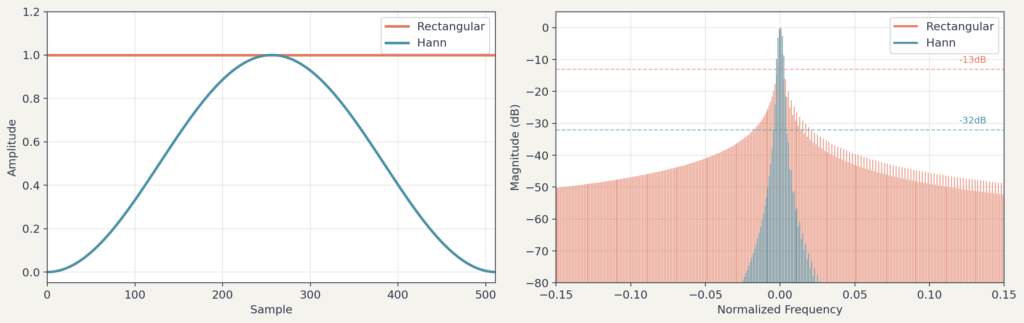
이 문제를 완화하기 위해 윈도우 함수(window fuction)를 사용합니다. 윈도우 함수는 구간의 중앙은 그대로 두고 양 끝을 부드럽게 $0$으로 줄여주는 함수입니다. 가장 많이 쓰이는 것은 한(Hann) 윈도우 입니다.

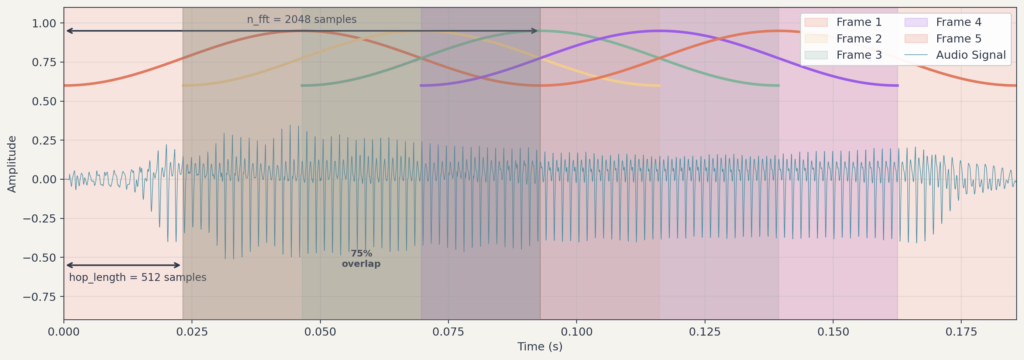
홉 길이와 겹침

윈도우를 얼마나 이동시키며 분석할지를 결정하는 것이 홉 길이(hop length)입니다. 윈도우 크기가 1024 샘플이고 홉 길이가 512 샘플이면, 인접한 두 프레임은 절반이 겹칩니다. 홉 길이가 작을수록 시간 해상도가 높아지지만 계산량이 늘어납니다.

시간-주파수 해상도 트레이드오프

윈도우 크기(n_fft)는 한 프레임의 샘플 수 입니다. 클수록 주파수 해상도가 높아지지만 시간 해상도는 낮아집니다. 시간 해상도와 주파수 해상도를 동시에 높일수는 없습니다.

이것이 시간-주파수 해상도의 트레이드오프입니다. 시간 해상도와 주파수 해상도를 동시에 높일 수는 없습니다. 구체적으로, 시간 간격은 $\text{hop\_length}/sr$ 초, 주파수 간격은 $sr/n_\text{fft}$ $\text{Hz}$입니다.

STFT 전체 흐름

지금까지 설명한 개념들이 실제로 어떻게 결합되는지 살펴봅시다. 샘플레이트 $\text{22,050Hz}$ 기준으로 $\text{n\_fft=2048}$, $\text{hop\_length=512}$를 사용한다고 가정하겠습니다. 이 값은 librosa의 기본값으로, 문서에서 음악 신호 분석에 적합하다고 안내합니다.²

• 각 프레임은 약 $\text{93ms (2048/22050)}$ 길이의 신호를 분석합니다
• 프레임은 약 $\text{23ms (512/22050)}$ 간격으로 이동하며, 인접 프레임과 $\text{75\%}$ 겹칩니다
• 한(Hann) 윈도우를 적용하여 경계를 부드럽게 처리한 뒤 FFT를 수행합니다
• 각 프레임마다 주파수 스펙트럼이 산출되고, 이를 시간 순서로 나열하면 스펙트로그램이 됩니다
  

STFT 수식

윈도우 함수 $w[n]$을 적용한 STFT는 다음과 같이 정의됩니다.

각 기호의 의미는 다음과 같습니다.

• $m:$프레임 인덱스 (시간 축)
• $k:$주파수 빈(FFT의 각 인덱스가 대응하는 주파수 구간) 인데스 (주파수 축)
• $H:$홉 길이
• $N:$윈도우 크기 (n_fft)

샘플링 레이트가 $sr$이고 FFT 크기가 $n_\text{fft}$ 일 때, $k$번째 주파수 빈은 $f_k=k \cdot sr / n_\text{fft}$ $\text{Hz}$에 대응합니다.

이 글에서는 단순화를 위해 $N = \text{win\_length} = \text{n\_fft}$인 경우를 가정합니다. 일반 구현에서는$\text{win\_length} \;\le \; \text{n\_fft}$로 두고, 윈도우 함수를 적용한 뒤 $0$ 패딩하여 FFT를 계산하기도 합니다.

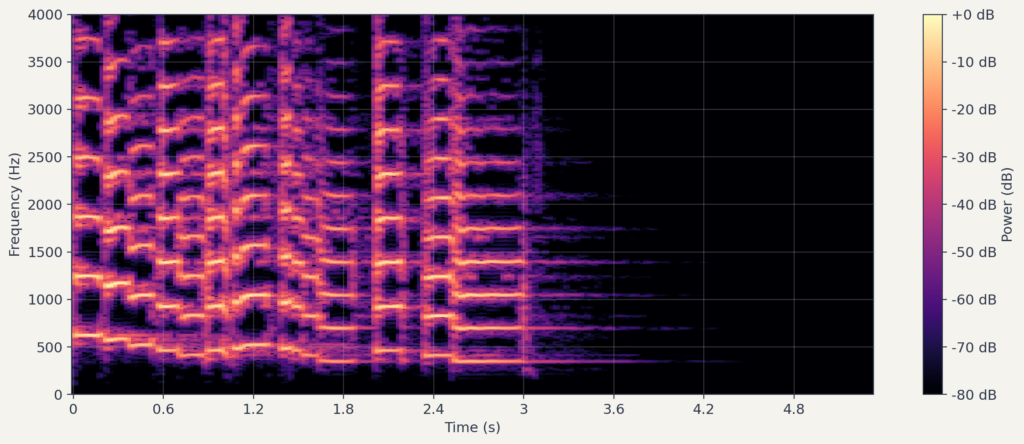
$|X[m,k]|^2$를 모든 $m$, $k$에 대해 계산하면, 시간-주파수 평면 위에 에너지 분포가 그려집니다. 이것이 스펙트로그램(spectrogram)입니다.

이하에서는 파워 스펙트로그램을 $\mathbf{P} \in \mathbb{R}^{d \times t}$로 표기합니다. 여기서 $d = 1 + \lfloor n_{\text{fft}} /2 \rfloor$는 실수 입력 STFT의 주파수 빈 수이고, $t$는 시간 프레임 수입니다. 행은 주파수 축, 열은 시간 축에 대응합니다.

3. 멜 스케일: 사람처럼 듣기

청각심리학적 배경

스펙트로그램의 주파수 축은 선형입니다. $\text{0Hz}$, $\text{100Hz}$, $\text{200Hz}$, … 같은 간격으로 나뉘어 있습니다. 하지만 사람의 귀는 주파수를 선형으로 인식하지 않습니다.

$\text{1000Hz}$에서 $\text{1100Hz}$로 바뀌는 것과 $\text{100Hz}$ 에서 $\text{200Hz}$로 바뀌는 것은 비교해보면, 물리적으로는 둘 다 $\text{100Hz}$ 차이이지만 실제로 느끼는 음높이 변화는 후자가 훨씬 큽니다. 저주파 영역에서는 작은 주파수 차이도 크게 느껴지고, 고주파 영역에서는 큰 차이도 잘 구분하지 못합니다.

이러한 청각 특성을 반영한 것이 멜 스케일(Mel scale)입니다. 멜 스케일에서 동일한 간격은 사람에게 동일한 음높이 차이로 지각됩니다.

멜 변환 공식

주파수를 멜로 변환하는 공식은 여러 버전이 있습니다. 대표적으로 HTK 스타일과 Slaney 스타일이 있으며, 라이브러리마다 기본값이 다릅니다. 이 글에서는 수식과 코드의 일관성을 위해 HTK 스타일을 사용합니다.³

주파수 $f(Hz)$를 멜 $m$으로 변환하는 HTK 공식은 다음과 같습니다.

역변환은 다음과 같습니다.

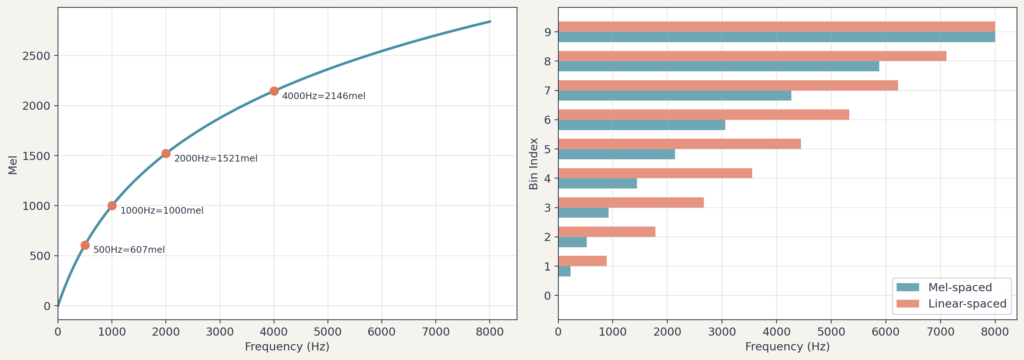
이 공식을 그래프로 그리면, 저주파 영역은 촘촘하게, 고주파 영역은 넓게 펼쳐지는 것을 볼 수 있습니다. 사람의 귀가 저주파를 더 세밀하게 구분하는 특성을 반영합니다.

멜 필터 뱅크

스펙트로그램을 멜 스케일로 바꾸려면 멜 필터 뱅크(Mel filter bank)를 사용합니다. 필터 뱅크는 여러 개의 삼각형 필터로 구성됩니다.

1. 멜 스케일 위에서 등간격으로 중심 주파수를 정합니다. (예:128개).
2. 각 중심 주파수에 삼각형 필터를 배치합니다.
3. 이 필터들을 원래 주파수 축으로 역변환하면, 저주파에는 좁은 필터가, 고주파에는 넓은 필터가 배치됩니다.
   
   

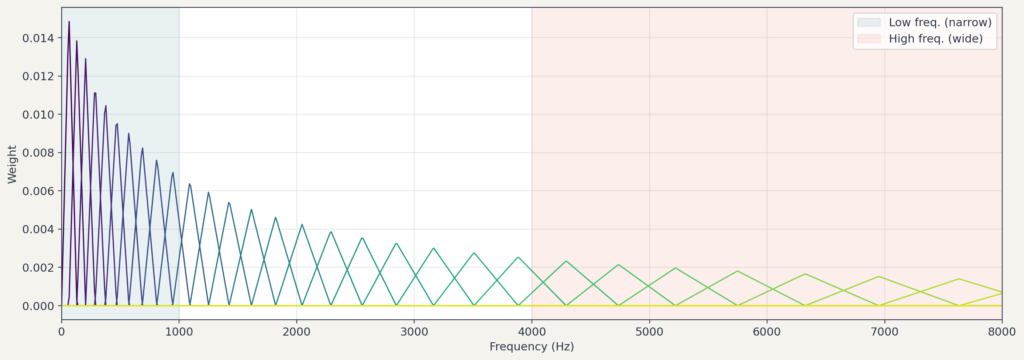
멜 밴드 수 n_mels 는 라이브러리 기본값이 $\text{128}$인 경우가 많고, n_mels가 커질수록 멜 축의 해상도가 높아지는 대신 입력 차원과 계산량도 증가합니다.

주파수 빈(frequency bin)은 FFT 결과의 각 인덱스가 대응하는 주파수 구간입니다. 멜 빈은 이와 달리 멜 필터 뱅크의 각 밴드가 여러 주파수 빈을 가중합하여 만든 출력입니다.

스펙트로그램의 각 프레임에 이 필터들을 적용하면, 기존의 수천 개 주파수 빈이 수십~수백 개의 멜 빈으로 압축됩니다. 이 과정에서 사람이 잘 구분하지 못하는 고주파의 세부 정보는 뭉쳐지고, 민감하게 반응하는 저주파 정보는 보존됩니다.

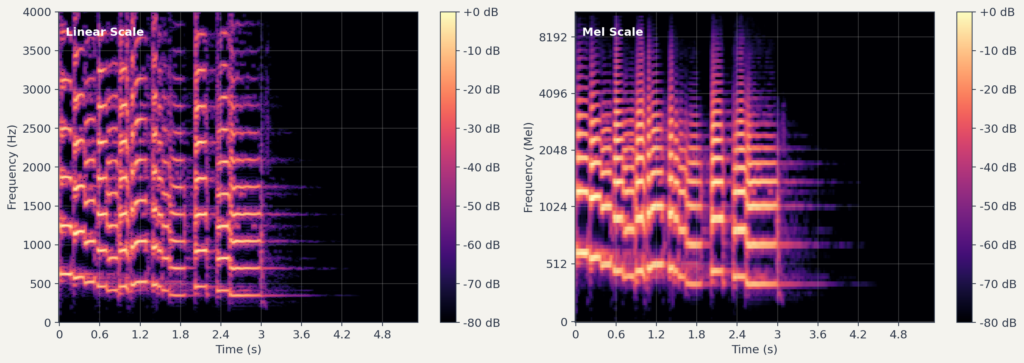
수식으로 표현하면, 필터 뱅크 행렬을 $\mathbf{M} \in \mathbb{R}^{n_{\text{mels}} \times d}$, 파워 스펙트로그램을 $\mathbf{P} \in \mathbb{R}^{d \times t}$라고 할 때, 멜 스펙트로그램 $\mathbf{S}_{\text{mel}} \in \mathbb{R}^{n_{\text{mels}} \times t}$은 다음과 같이 계산됩니다.

여기서 $d = 1 + \lfloor n_{\text{fft}}/2 \rfloor$는 주파수 빈 수, $t$는 시간 프레임 수, $n_{\text{mels}}$는 멜 빈 수입니다.

4. 멜 스펙트로그램 생성

전체 파이프라인

이 글과 이후의 코드 예시는 파워 스펙트럼(power spectrum, 진폭의 제곱)을 기준으로 멜 스펙트로그램을 구성합니다. 진폭(amplitude) 기반으로 작업할 경우 dB 변환 공식이 달라지므로($\text{20 log}_{10}$ 계열) 주의가 필요합니다. 또한 파워 스펙트럼의 스케일 상수(윈도우 보정, 정규화 등)는 구현마다 다를 수 있습니다.

멜 스펙트로그램을 만드는 전체 과정을 정리하면 다음과 같습니다.

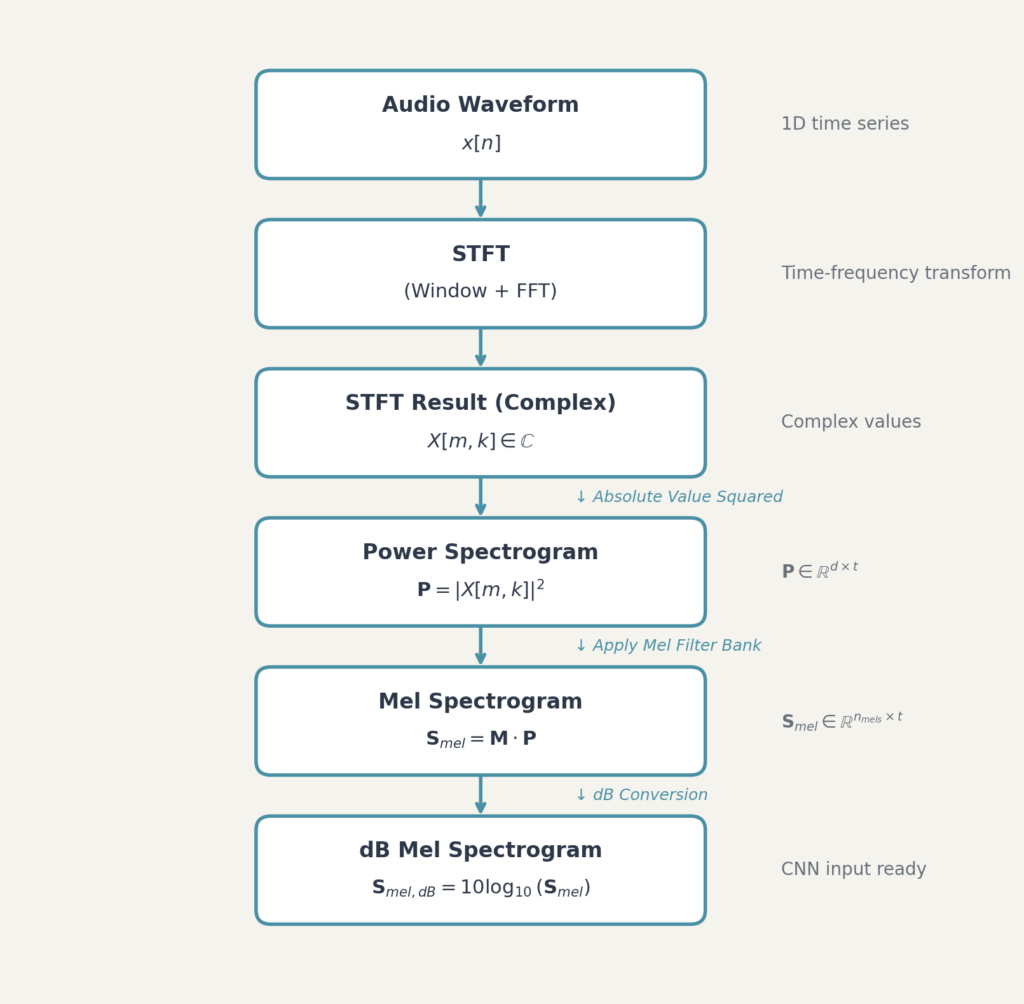
dB 변환의 이유

마지막 단계에서 dB(데시벨) 변환을 하는 이유는 무엇일까요?

데시벨은 두 값의 비율을 로그 스케일로 표현하는 단위입니다. 원래 전력(power) 비율을 다루기 위해 만들어졌으며, 큰 동적 범위를 압축하여 다루기 쉽게 만들어줍니다.

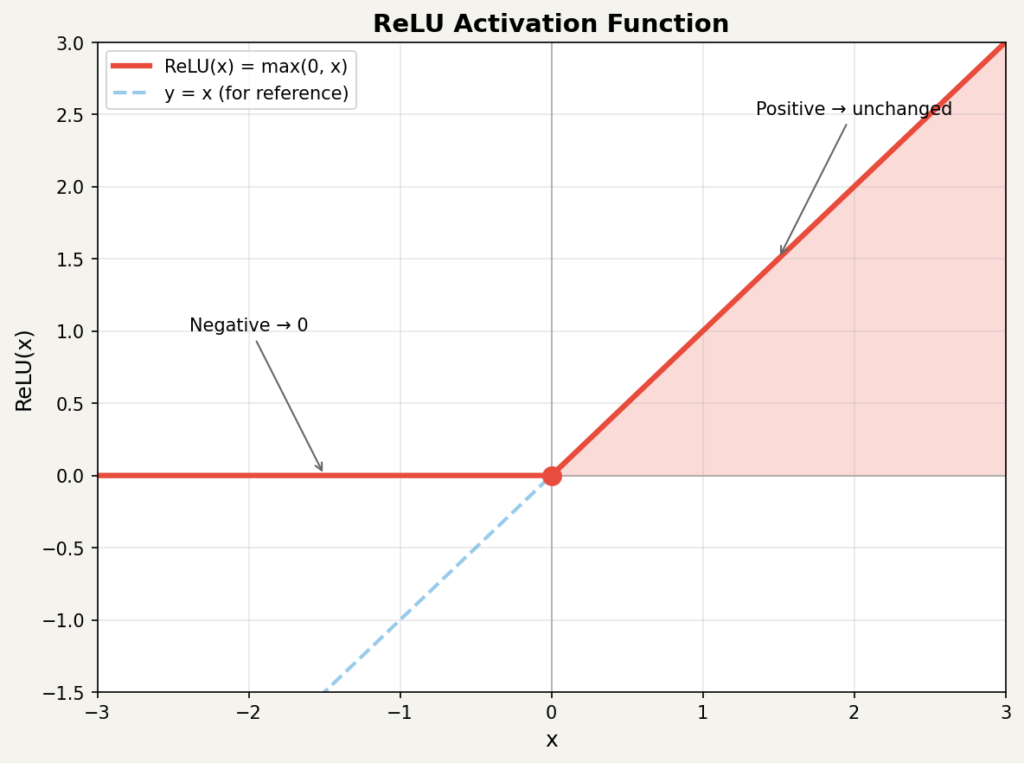
첫째, 사람의 청각은 소리의 세기를 대략 로그 스케일에 가깝게 인식합니다. dB 변환은 이러한 청각 특성과 방향이 맞아, 지각적으로 의미 있는 차이를 더 잘 반영합니다.

둘째, 오디오 신호의 에너지는 범위가 매우 넓습니다. 가장 큰 값과 작은 값의 차이가 수백만 배에 이를 수 있습니다. dB 변환을 거치면 이 범위가 압축되어, 신경망이 학습하기 쉬운 형태가 됩니다.

파워 스펙트럼에 대한 dB 변환은 다음과 같이 정의됩니다. 실제 구현에서는 수치 안정성을 위해 입력에 하한($a_{min}$)을 적용합니다.

librosa의 power_to_db 는 이 공식을 구현하며, 추가로 top_db 파라미터로 출력의 동적 범위를 제한합니다.

여기서 ref는 기준값입니다. ref=np.max 를 사용하면 각 샘플의 최대값이 $\text{0dB}$가 되는 상대 스케일로 변환됩니다. 이 경우 모든 값은 $0$이하의 음수가 되며, top_db=80(기본 값)이면 바닥값은 $\text{-80dB}$근처로 제한됩니다.

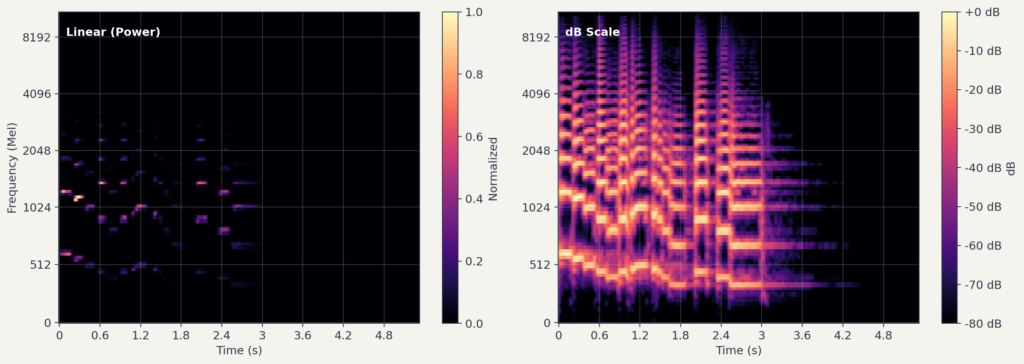
5. CNN 입력용 후처리

멜 스펙트로그램을 이미지 기반 모델에 넣으려면 몇 가지 추가 처리가 필요합니다. 이 글에서는 CNN을 예로 들어 설명하며, dB 멜 스펙트로그램 $\mathbf{S}_{\text{mel, dB}}$를 사용한다고 가정합니다.

크기 고정

CNN은 보통 고정된 입력 크기를 기대합니다. 하지만 오디오 파일의 길이는 제각각이므로, 멜 스펙트로그램의 시간 축 길이도 다릅니다.

해결 방법은 여러 가지가 있습니다.

• 자르기(crop): 긴 오디오는 일정 길이로 자름
• 패딩(padding): 짧은 오디오는 특정 값으로 채움
• 리사이즈(resize): 보간(interpolation)으로 크기 조정. 단, 시간 축이 왜곡될 수 있어 해석 관점에서 주의가 필요합니다. 분류 성능만을 목적으로 할 때 주로 사용됩니다.

연구에 따라 다르지만, 많은 경우 오디오를 일정 길이(예:3초)로 자른 뒤 멜 스펙트로그램을 생성합니다. 이렇게 하면 모든 입력의 크기가 동일해집니다. 일반적으로 crop이나 padding을 우선 고려하고, resize는 필요한 경우에 한해 사용합니다.

패딩을 사용할 경우, 파형 또는 파워 스펙트럼 단계에서 수행하는 것이 안전합니다. $\text{dB}$멜 스펙트로그램에서는 $0$ 패딩을 피해야 합니다.⁴

채널 처리

멜 스펙트로그램은 기본적으로 단일 채널(흑백 이미지와 유사)입니다. 하지만 ImageNet 등에서 사전 학습된 CNN 모델들은 3채널(RGB) 입력을 기대합니다.

흔한 해결책은 같은 $\text{dB}$ 멜 스펙트로그램을 3번 복제하여 3채널로 만드는 것입니다. 또한 델타 및 델타-델타처럼 시간 변화 정보를 담은 특징을 별도 채널로 구성하는 방법도 있습니다.⁵

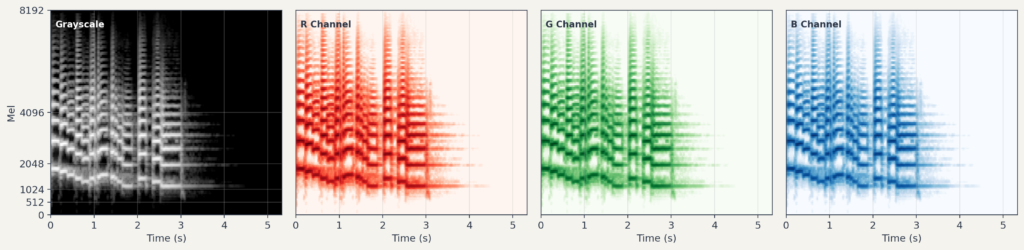
값 정규화

신경망 학습을 안정화하려면 입력 값의 범위를 조정해야 합니다.

Min-Max 정규화: 값을 $\text{0\textasciitilde1}$ 범위로 조정

표준화(Standardization): 평균 $0$, 표준편차 $1$로 조정

데이터 누수를 피하려면 $x_{\min}, x_{\max}$ 또는 $\mu$, $\sigma$는, 학습(train) 세트에서만 추정하고, 검증 및 테스트에는 동일 값을 적용해야 합니다.

정규화와 패딩의 상호작용 주의: 패딩값이 정규화 통계에 포함되면 유효 데이터의 대비(contrast)가 무너질 수 있습니다. 정규화 통계는 패딩 영역을 제외하고 계산(마스크)하거나, 정규화를 먼저 수행한 뒤 패딩하는 방식을 권장합니다.

사전 학습된 모델을 사용할 때는 해당 모델의 입력 전처리를 맞추는 것이 기본 전략입니다(예:ImageNet 평균/표준편차). 다만 스펙트로그램은 자연 이미지와 분포가 다르기 때문에, 별도의 정규화가 더 안정적인 경우도 있습니다. 실험을 통해 검증하는 것을 권장합니다.

6. 코드 예시 (librosa)

Python의 librosa 라이브러리를 사용하면 멜 스펙트로그램을 쉽게 생성할 수 있습니다. 아래 코드는 재현성을 위해 기본값을 포함한 주요 파라미터를 명시적으로 지정합니다.

import librosa
import librosa.display
import numpy as np
import matplotlib.pyplot as plt

# 오디오 로드
y, sr = librosa.load('audio.wav', sr=22050)  # sr: 샘플링 레이트 (일반: 16000, 22050, 44100)

# 멜 스펙트로그램 생성
mel_spec = librosa.feature.melspectrogram(
    y=y,
    sr=sr,
    # STFT 파라미터
    n_fft=2048,          # FFT 크기 — 주파수 해상도 결정 (일반: 1024, 2048)
    hop_length=512,      # 홉 길이 — 시간 해상도 결정 (일반: n_fft/4)
    win_length=None,     # 윈도우 길이 — None이면 n_fft와 동일
    window='hann',       # 윈도우 함수 — 스펙트럼 누설 방지
    center=True,         # 프레임 중앙 정렬 (각주 참조)
    pad_mode='constant',
    # 스펙트럼 설정
    power=2.0,           # 2.0=파워, 1.0=진폭 — dB 공식에 영향 (10 vs 20 log)
    # 멜 필터 뱅크 파라미터
    n_mels=128,          # 멜 빈 수 (일반: 64, 128, 256)
    fmin=0,              # 최소 주파수 (Hz)
    fmax=None,           # 최대 주파수 — None이면 sr/2
    htk=True,            # HTK 멜 스케일 — 본문 수식과 일치 (librosa 기본값은 False)
    norm='slaney'        # 필터 정규화 방식
)

# dB 변환
mel_db = librosa.power_to_db(
    mel_spec,
    ref=np.max,          # 상대 스케일 — 최대값이 0dB (패딩 시 주의, 각주 참조)
    amin=1e-10,          # 로그 클리핑 — log(0) 방지
    top_db=80            # 동적 범위 제한 — 바닥값 = 최대값 - 80dB
)

# 시각화
plt.figure(figsize=(10, 4))
librosa.display.specshow(
    mel_db,
    sr=sr,
    hop_length=512,
    x_axis='time',
    y_axis='mel',
    htk=True             # 시각화에서도 HTK 스케일 사용
)
plt.colorbar(format='%+2.0f dB')
plt.title('Mel Spectrogram (dB)')
plt.tight_layout()
plt.show()

import librosa
import librosa.display
import numpy as np
import matplotlib.pyplot as plt

# 오디오 로드
y, sr = librosa.load('audio.wav', sr=22050)  # sr: 샘플링 레이트 (일반: 16000, 22050, 44100)

# 멜 스펙트로그램 생성
mel_spec = librosa.feature.melspectrogram(
    y=y,
    sr=sr,
    # STFT 파라미터
    n_fft=2048,          # FFT 크기 — 주파수 해상도 결정 (일반: 1024, 2048)
    hop_length=512,      # 홉 길이 — 시간 해상도 결정 (일반: n_fft/4)
    win_length=None,     # 윈도우 길이 — None이면 n_fft와 동일
    window='hann',       # 윈도우 함수 — 스펙트럼 누설 방지
    center=True,         # 프레임 중앙 정렬 (각주 참조)
    pad_mode='constant',
    # 스펙트럼 설정
    power=2.0,           # 2.0=파워, 1.0=진폭 — dB 공식에 영향 (10 vs 20 log)
    # 멜 필터 뱅크 파라미터
    n_mels=128,          # 멜 빈 수 (일반: 64, 128, 256)
    fmin=0,              # 최소 주파수 (Hz)
    fmax=None,           # 최대 주파수 — None이면 sr/2
    htk=True,            # HTK 멜 스케일 — 본문 수식과 일치 (librosa 기본값은 False)
    norm='slaney'        # 필터 정규화 방식
)

# dB 변환
mel_db = librosa.power_to_db(
    mel_spec,
    ref=np.max,          # 상대 스케일 — 최대값이 0dB (패딩 시 주의, 각주 참조)
    amin=1e-10,          # 로그 클리핑 — log(0) 방지
    top_db=80            # 동적 범위 제한 — 바닥값 = 최대값 - 80dB
)

# 시각화
plt.figure(figsize=(10, 4))
librosa.display.specshow(
    mel_db,
    sr=sr,
    hop_length=512,
    x_axis='time',
    y_axis='mel',
    htk=True             # 시각화에서도 HTK 스케일 사용
)
plt.colorbar(format='%+2.0f dB')
plt.title('Mel Spectrogram (dB)')
plt.tight_layout()
plt.show()

power_to_db 함수 설명

librosa.power_to_db 는 파워 스펙트로그램을 $\text{dB}$ 스케일로 변환합니다. 내부적으로 10 * log10(max(S, amin) / ref 형태의 계산을 수행합니다.

• ref=np.max: 각 입력의 최대값을 기준으로 상대 $\text{dB}$를 계산합니다. 최대값이 $\text{0dB}$가 되고, 나머지는 음수값이 됩니다.
• ref=1.0: 절대 기준을 사용합니다. 입력 스케일에 따라 값의 범위가 달라집니다.
• amin: 입력의 하한값. np.maximum(amin, S) 형태로 클리핑하여 로그의 $0$ 입력을 방지합니다.
• top_db: 출력의 동적 범위 제한. 기본값이 $80$이면 최대값에서 $\text{-80dB}$ 이하는 잘립니다.

데이터셋 간 비교가 필요하거나 절대적인 음량 정보가 중요한 경우, ref 설정에 주의해야 합니다.

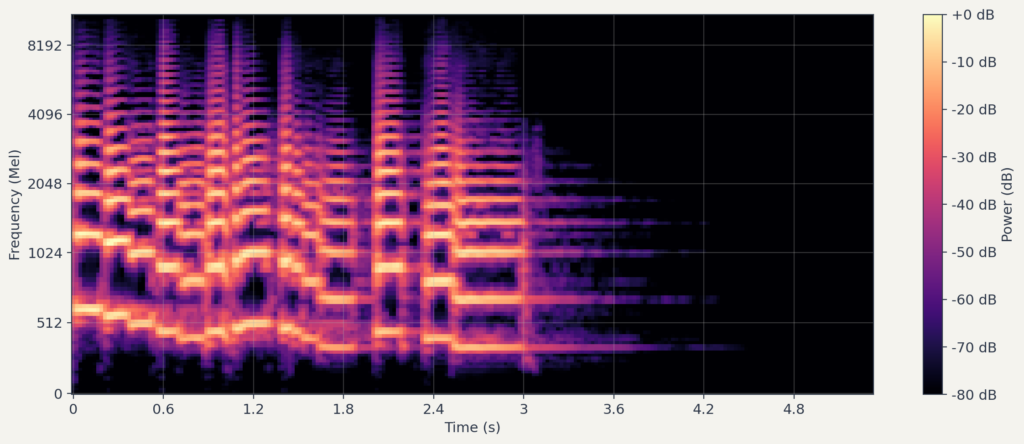
마무리

멜 스펙트로그램은 오디오 신호를 CNN이나 Vision Transformer 등 이미지 기반 모델이 처리할 수 있는 2차원 이미지로 변환하는 표현입니다. 생성 과정을 요약하면 다음과 같습니다.

1. STFT: 시간-주파수 분석으로 스펙트로그램 생성
2. 멜 필터 뱅크: 사람의 청각 특성을 반영한 주파수 축 변환
3. $\text{dB}$ 변환: 에너지의 동적 범위 압축 ($\text{10 log}_{10}$ 스케일)
4. 후처리: 크기 고정, 채널 복제, 정규화

이 글의 모든 수식과 코드는 파워 스펙트럼(진폭의 제곱) 기준이며, 멜 스케일은 HTK 스타일(htk=True)을 따릅니다. 진폭 기반으로 작업할 경우 $\text{dB}$ 공식이 달라지고($\text{20 log}_{10}$), $\text{Slaney}$ 스타일 멜 스케일을 사용할 경우 변환 공식이 달라지므로 참고 바랍니다.

이렇게 만들어진 멜 스펙트로그램은 AI 생성 음악 탐지, 음성 인식, 음악 장르 분류 등 다양한 오디오 딥러닝 태스크에서 가장 널리 쓰이는 입력 표현 중 하나입니다.

실습 코드

아래 레포지토리에서 본문의 각 단계를 직접 실행해볼 수 있습니다. 푸리에 변환, STFT, 멜 필터 뱅크, dB 변환, CNN 전처리까지 6개 모듈로 구성되어 있고, config.yaml에서 파라미터를 바꿔가며 결과 차이를 눈으로 확인할 수 있습니다.

https://github.com/ToleranceKim/mel-spectrogram-tutorial

참고문헌

Stevens, S. S., Volkmann, J., & Newman, E. B. (1937). A scale for the measurement of the psychological magnitude pitch. The Journal of the Acoustical Society of America, 8(3), 185-190. (멜 개념의 심리음향적 기원)

Slaney, M. (1998). Auditory Toolbox. Version 2. Technical Report #1998-010, Interval Research Corporation. https://engineering.purdue.edu/~malcolm/interval/1998-010/ (Slaney 스타일 멜 필터뱅크)

Young, S., Evermann, G., Gales, M., Hain, T., Kershaw, D., Liu, X., Moore, G., Odell, J., Ollason, D., Povey, D., Valtchev, V., & Woodland, P. (2006). The HTK Book (Version 3.4). Cambridge University Engineering Department. (HTK식 멜 변환 공식, 델타/가속도 계수)

Oppenheim, A. V., & Schafer, R. W. (2009). Discrete-Time Signal Processing (3rd ed.). Pearson. (DFT/STFT 수식, 파워 스펙트럼 정의)

Harris, F. J. (1978). On the use of windows for harmonic analysis with the discrete Fourier transform. Proceedings of the IEEE, 66(1), 51-83. (스펙트럼 누설, 윈도우 함수, Hann 윈도우 수식)

librosa.stft: https://librosa.org/doc/latest/generated/librosa.stft.html

librosa.feature.melspectrogram: https://librosa.org/doc/latest/generated/librosa.feature.melspectrogram.html

librosa.feature.delta: https://librosa.org/doc/latest/generated/librosa.feature.delta.html

librosa.power_to_db: https://librosa.org/doc/latest/generated/librosa.power_to_db.html

librosa.filters.mel: https://librosa.org/doc/latest/generated/librosa.filters.mel.html

1. DFT를 정의대로 계산하면 연산량이 샘플 수의 제곱에 비례( $O(N^{2})$ )이지만, FFT는 이를 $\text{샘플 수}\times log$ 수준( $O(N\ log\ N)$ )으로 줄입니다. ↩︎
2. librosa.stft 문서 원문: “The default value, n_fft=2048 samples, corresponds to a physical duration of 93 milliseconds at a sample rate of 22050 Hz. This value is well adapted for music signals. However, in speech processing, the recommended value is 512.” (https://librosa.org/doc/0.10.2/generated/librosa.stft.html) ↩︎
3. HTK 스타일은 멜 주파수 변환 공식 선택(htk=True)을 의미합니다. 필터 가중치 정규화(norm)는 별도 설정이며, 이 글의 코드에서는 librosa 기본값(norm='slaney')을 따릅니다. melspectrogram은 내부적으로 librosa.filters.mel을 호출하여 필터 뱅크를 생성합니다. librosa의 기본값은 Slaney 스타일(htk=False)이며, Slaney 계열은 저주파 구간(대략 $\text{1kHz}$ 이하)을 선형에 가깝게 매핑하는 방식으로 HTK의 완전 로그형과 미세한 차이가 있습니다. 재현성이 중요한 경우 옵션을 명시하는 것이 좋습니다. ↩︎
4. 파형에서는 $0$ 패딩이 가능합니다($0$은 무음). 파워 멜 스펙트로그램에서도 $0$ 패딩이 가능합니다($0$은 에너지 없음, $\text{dB}$ 변환 시 amin 으로 클리핑). $\text{dB}$ 멜 스펙트로그램에서는 ref=np.max 처럼 $\text{0dB}$가 최대 에너지로 정의되는 설정에서 $\text{0}$ 패딩을 피해야 합니다. $\text{dB}$ 스케일 에서 $0$은 ‘무음’이 아니라 ‘기준 대비 동일 에너지’를 의미하므로, $0$으로 채우면 패딩 구간이 최대값처럼 해석될 수 있습니다. 대신 -top_db 수준(예:$\text{-80dB}$)이나 mel_db.min()을 사용하세요. 또한 librosa는 기본적으로 center=True로 동작하여 프레임 중앙 정렬을 위해 입력에 패딩을 추가합니다. 프레임의 시간 기준을 샘플 인덱스와 맞춰야 하는 경우(onset 검출 등)에는 center=False 를 검토하세요. ↩︎
5. 멜 스펙트로그램(정적 특징), 델타(시간 축 1차 변화율 근사), 델타-델타(시간 축 2차 변화율 근사, 가속도)를 각 채널에 배치하는 방식입니다. 전통적인 음성 인식 파이프라인에서는 MFCC에 델타 및 델타-델타 계수를 추가하는 구성이 관행적으로 널리 사용되어 왔습니다. librosa에서는 librosa.feature.delta() 로 계산할 수 있으며, 이 함수는 단순 차분이 아닌 $\text{Savitzky-Golay}$ 필터 기반으로 변화량을 근사합니다. ↩︎